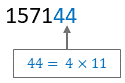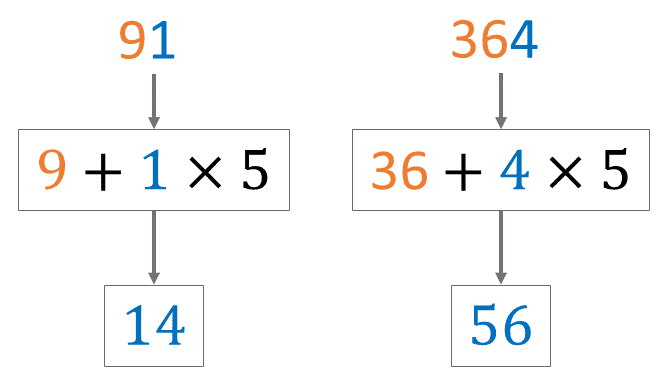في عالم الرياضيات، يعتبر فهم قابلية القسمة على الأعداد من 2 إلى 10 أساسياً لتحليل الأعداد وتبسيط العمليات الحسابية. يمكننا تبسيط هذه المهمة بشكل كبير من خلال استغلال خصائص رقمية محددة. توفر هذه الخصائص طرقًا عملية وسريعة لفحص قابلية القسمة دون الحاجة لإجراء حسابات معقدة.
قابلية القسمة على: 2
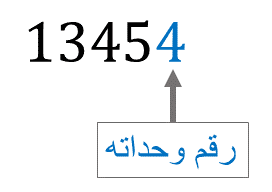
يكون عدد صحيح طبيعي قابلا للقسمة على 2 إذا كان رقم وحداته زوجي
والأرقام الزوجية هي 0 , 2 , 4 , 6 , 8 , 10
مثال
- 13454 يقبل القسمة على 2 لأن رقم وحداته هو 4 و4 عدد زوجي.
قابلية القسمة على: 3
- يكون عدد صحيح طبيعي قابل للقسمة على 3 إذا كان
<مجموع أرقامة يقبل القسمة على 3>.
مثال
- 12352 يقبل القسمة على 3 لآن :
- و يقبل القسمة على 3
قابلية القسمة على: 4
يكون عدد صحيح طبيعي قابلا للقسمة على 4 إذا كان
<العدد المكون من رقم وحداته وعشراته يقبل القسمة على 4 >الأعداد المكونة من رقمين وقابلة للقسمة على 4 هي :
- إذا كان رقم العشرات عددا زوجيا, ورقم الوحدات هو 0 أو 4 أو 8
- إذا كان رقم العشرات عددا فرديا, ورقم الوحدات هو 2 أو 6.
مثال
- 134544 يقبل القسمة على 4 لأن العدد 44 يقبل القسمة على 4
قابلية القسمة على: 5
- يكون عدد صحيح طبيعي قابلا للقسمة على 5 إذا كان رقم وحداته 0 أو 5
مثال
- 7505 يقبل القسمة على 5 لأن رقم وحداته هو 5
قابلية القسمة على: 6
- يكون عدد صحيح طبيعي قابلا للقسمة على 6 إذا كان يقبل القسمة على 2 وعلى 3.
مثال
-
252 يقبل القسمة على 2 لأن
- رقم وحداته هو 2 عدد زوجي
- و يقبل القسمة على ثلاتة لأن مجموع أرقامه :
- عدد يقبل القسمة على 3
قابلية القسمة على: 7
يكون عدد صحيح طبيعي قابلا للقسمة على 7 إذا كان العدد الذي يساوي :
- العدد المكون من جميع أرقامه ابتداء من عشراته (بنفس الترتيب, نحذف فقط رقم الوحدات) زائد رقم وحداته ضرب 5
- يقبل القسمة على 7.
ملاحظة
الطريقة من إبداع الطالب النيجيري “Chika Ofili”ذو الاثني عشر عامًا
مثال
-
العددان 14 و 56 يقبلان القسمة على 7 إدن العددان 91 و 364 كدالك يقبلان القسمة على 7
-
وفي الواقع إذا كررت العملية مع النواتج ستنتهي بالرقم 7 أو بالعدد 49؛ وذلك إذا كان العدد الأصلي يقبل القسمة على 7. مثال مع العدد :
- العدد يقبل القسمة على 7
قابلية القسمة على: 8
- يكون عدد صحيح طبيعي قابلا للقسمة على 8 إذا كان قابلا للقسمة على 2 ونصفه يقبل القسمة على 4.
مثال
1264 يقبل القسمة على 8 لأنه
- يقبل القسمة على 2 (رقم وحداته هو 4)
- و 632 يقبل القسمة على 4 (32 يقبل القسمة على 4)
يكون عدد صحيح طبيعي قابلا للقسمة على 8 إذا كان العدد المكون من
<رقم وحداته وعشراته ومئاته يقبل القسمة على 8>مثال
1459632 يقبل القسمة على 8 لآن 632 يقبل القسمة على 8
قابلية القسمة على: 9
يكون عدد صحيح طبيعي قابل للقسمة على 9 إذا كان
<مجموع أرقامة يقبل القسمة على 9>مثال
- 13456 يقبل القسمة على 9 لأن :
- مجموع أرقامه
- 18 يقبل القسمة على 9
قابلية القسمة على: 10
يكون عدد صحيح طبيعي قابلا للقسمة على 10 إذا كان رقم <وحداته هو 0>مثال
- العدد 357690 يقبل القسمة على 10